Aqui segue uma ajuda pros amigos da sala Parlamento no Kongregate (e também pra todos os curiosos e necessitados de passagen) sobre o jogo Hexiom.
Estágio 16
(desculpem a qualidade da imagem, tirei o print depois de ter concluído o estágio)
Estágio 17
Estágio 18 (trocar a peça 4 com a 3)
Estágio 19
Estágio 20
Estágio 21
Estágio 22
Estágio 23
Falta o resto, editarei noutra hora :P
terça-feira, 15 de novembro de 2011
terça-feira, 12 de julho de 2011
Quem pode
Original: Who Can Name the Bigger Number?
by Scott Aaronson
[Author's blog]
Em uma antiga piada, dois nobres **vie** nomear/representar* o maior número. O primeiro, após ruminar por horas, triumfantemente anuncia "Oitenta e três!". O segundo, poderosamente impressionado, responde "Você venceu."
Uma competição do número maior é claramente sem sentido quando os participantes atuam por turnos alternados. Mas o que acontece se os competidores escrevem seus números simultaneamente, nenhum **aware of** outro? Para introduzir uma conversa sobre "Big Numbers," eu convidei dois voluntários para tentar exartamente isto. Digo a eles as regras:
Vocês têm quinze segundos. Usando notação matemática padrão, palavras em Inglês, ou ambos, representem um único número por extenso - não uma infinidade - em um ** index card / cartão-ficha** em branco. Sejam precisos o suficiente para qualquer matemático moderno determinar exatamente que número vocês representaram consultando apenas seu cartão e, se necessário, literatura publicada.
Então os competidores não podem dizer "o número de grãos de areia do Saara," porque areia sai e entra no Saara regularmente. Também não podem dizer "o número do meu oponente mais um" ou "o maior número que qualquer pessoa já tenha pensado mais um" - novamente, estes número são mal definidos, dado o que nosso matemático razoavel tem disponivel. Dentro das regras, o competidor que representasse o maior número vence. Estão prontos? Preparar. Vão.
Os resultados da competição nunca foram como eu esperava. Uma vez, um garoto do sétimo ano encheu seu cartão com uma **string** de 9's sucessivos. Como muitos outros **big-number tyros**, ele procurou maximizar seu número enchendo um 9 em todo espaço disponivel. Se ele tivesse escolhido escrever 1's ao invés do 9 curvilíneo, seu número poderia ter sido milhões de vezes maior. Ele ainda teria sido **decimated**, no entanto, pela garota que ele estava competindo contra, que escreveu uma **string** de 9's seguido pelo sobrescrito 999. A-ha! um exponencial: um número multiplicado por si mesmo 999 vezes. Notando essa inovação, declarei a vitória da garota sem me importar contar os 9's nos cartões.
E, mesmo que o número da garota tivesse sido muito maior, seria maior ainda se ela tivesse **stacked** o exponencial mais do que uma vez. Take
por exemplo. este **behemoth**, igual a 9387,420,489, tem 369,693,100 dígitos. Por comparação, o número de partículas elementares no universo observavel tem **a meager** 85 dígitos. Três 9's, quando exponencialmente sobrepostos, já nos **lift** incompreensivamente além de toda a matéria que podemos observar - por um fator pr volta de 10369,693,015. E nós não dissemos nada sobre 
ou 
. **Place value**, exponenciais, exponenciais **stacked**: cada um pode expresar números grandes sem limite, e neste sentido eles são todos equivalentes. Mas os sistemas notacionais diferem dramaticamente nos números que eles conseguem expressar de maneira concisa. Isso é o que o limite de tempo de 15 segundos ilustra. Demora a mesma quantidade de tempo para escrever 9999, 9999, and - embora o primeiro número seja cotidiano, o segundo seja astronômico, e o terceiro hiper-mega astronômico. A chave para a competição do maior número não é escrita rápida, e sim um paradigma potente para capturar concisamente o número gargantuesco.
Tais paradigmas são raridades históricas. Achamos **a flurry** na anrtiguidade, **another flurry** no século vinte, e não muito entre esses dois períodos. Mas, quando um novo modo para expressar grandes números concisamente emerge de fato, é sempre como produto conjunto de uma grande revolução científica: matemática sistematizada, lógica formal, ciência da computação. **Revolutions this momentous**, como qualquer **Kuhnian** diria a você, apenas ocorrem sob determinadas condições sociais. Assim é a história dos números grandes uma história do progresso humano.
E dentro disso permanece um paralelo com outra história matemática. No seu livro **remarkable** e **underappreciated** A History of Pi, Petr Beckmann argumenta qu e a razão da circunferência para o diâmetro é "um espelho **quaint little** da história do homem." Nas raras sociedades onde ciência e razão encontraram refúgio - a antiga Atenas de **Anaxagoras** e **Hippias**, a Alexandria de **Erastostenes** e Euclides, a Inglaterra do século XVII de Nerwton e Wallis - matemáticos fizeram saltos tremendos no cálculo de pi. Em Roma e na Europa medieval, em contraste, o conhecimento do pi estagnou. Aproximações cruas como os 25/8 dos babilônios **held sway**.
Este mesmo padrão permanece, eu acho, para números grandes. Curiosidade e **openness lead to fascination** com números grandes, e para **the buoyant view** que nenhuma quantidade, seja o número de estrelas na galáxia ou o número de de mãos de bridge possíveis, é imenso demais para a mente enumerar. **Conversely**, ignorância e irracionalidade levaram ao fatalismo sobre números grandes. O historiador Ilan Vardi cita a palavra grega antiga 'yammkosioi,' ou areia-entos, coloquialmente significando um zilhão; assim como uma passagem da Olympic Ode II, **asserting** que "areia escapa da contagem."
Mas a areia não escapa da contagem, como Arquimedes reconheceu no século terceiro AC. Aqui está como ele iniciou The Sand-Reckoner, algo como um artigo de ciência pop endereçado ao rei de **Siracusa**:
(...) Há alguns (...) que pensam que o número de grãos de areia é infinito **in multitude** (...) de novo há alguns que, sem levar em conta como inifnitos, ainda pensam que nenhum número foi dado que seja grande o suficiente para exceder essa **multitude**(...) Mas tentarei mostrar a você [números que] excedem não apenas o número de massa de areia igual em magnitude ao de terra (...), mas também uma massa igual em magnitude ao universo.
Assim Arquimedes procedeu para mostrar, essencialmente usando o termo grego antigo miríade, significando dez mil, como uma base para exponenciais. Adotando um modelo comológico **prescient** de **Aristarchus**, no qual a "esfera de cinco estrelas" é vastamente maior do que a esfera n a qual a Terra orbita ao redor do Sol, Arquimedes obteve um limite superior de 1063para o número de grãos de areia necessários para preencher o universo (supostamente 1063 é o maior número com um nome americano padrão lexicográfico: vingintillion. Mas o **staid** vingintillion manteve **vigil lest/last it be encroached** sob o mais **whimsically-named** googol, ou 10100, e googolplex, ou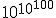
) . Por mais **vast - vasto** que fosse, é claro, 1063 não era **enshrined** como o maior n úmero de todos os tempos. Seis séculos depois, **Diophan tus - Diofanto** desenvolveu uma notação mais simples par a exponenciais, permitindo a ele ultrapassar 
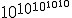. então, na Idade Média, a ascensão dos algarismos arábicos e **place value** facilitaram **to stack** exponenciais ainda mais alto. Mas o paradigma de Arquimedes para expressar números grandes não foi fundamentalmen te ultrapassada até o século vinte. E até mesmo hoje exponenciais dominam a discussão popular sobre **the im mense - a imensidão**.
Considere, por exemplo, a manjada lenda do Grão-vizir na Pérsia que inven tou o xadrez. O Rei, conforme diz a lenda, estava em deleite por causa do novo jogo e convidou o Vizir para **to name** sua própria recompensa. O Vizir respondeu que. sendo um homem modesto, desejava apenas um grão de trigo na primeira casa do tabuleiro de xadrez, dois grãos na segunda, quatro na terceira e assim por diante, com o dobro da quantidade de grãos da casa anterior na atual. O Rei **innumerate** concordou sem se dar conta que o total de grãos em todas as 64 casas seria de 264-1, ou 18.6 quintilhões - o equivalente à produção atual de trigo por 150 anos.
De maneira adequada, este crescimemnto exponencial é o que faz o próprio xadrez tão dificil. Há apenas 35 escolhas legalmente aceitas para cada movimento no xadrez, mas as escolhas multiplicam exponencialmente para **to yield** mais de 1050movimentos possíveis - movimentos demais para até mesmo um computador procurar exaustivamente. Isto é o que levou até 1997 para um computador, Deep Blue, derrotar o campeão mundial humano de xadrez. E em Go, que tem um tabuleiro de 19x19 casas e mais de 10150posições possíveis, até mesmo um humano amador pode **to rout** o programa de computador na posição mais alta do ranking. Crescimento exponencial **to plague** computadores em outros **guises** também. O problema do caixeiro viajante pede a rota mais curta conectando um conjunto de cidades, dadas as distâncias entre cada par de cidades. **The rub** é que o número de rotas possíveis cresce exponencialmente com o número de cidades. Quando há, digamos, 100 cidades, há por volta de 10158rotas possíveis e, embora vários atalhos sejam possíveis, nenhum algoritmo para computador é fundamentalmente melhor do que checar rotas uma a uma (método de força bruta). O problema do caixeiro viajante pertence a uma classe chamada NP-completa, a qual inclui centenas de outros problemas de interesse prático (NP representa o termo técnico "Tempo Polinomial Não-Determinístico"). É sabido que, se há algum algoritmo eficiente para algum problema NP-completo, então há algoritmos eficientes para todos eles. Aqui "eficiente" significa que, usando uma quantidade de tempo proporcional de, no máximo, o tamanho do problema elevado a algum expoente fixo - por exemplo, o núm ero de cidades ao cubo - . É conjecturado, no entantom que nenhum algoritmo para problemas NP-completos exista. Provando esta conjectura, chamada P = NP, tem sido um grande problema não-solucionado da Ciência da Computação por trinta anos.
Embora computadores provavelmente nunca resolvam problemas NP-completos eficientemente , há mais esperança para outro **grail - cálice/cálice sagrado** da Ciência da Computação: replicar a inteligência humana. O cérebro humano tem aproximadamente um bi lhão de neurônios ligados por cem trilhões de sinapses. E, apesar da função de um único neurônio ser apenas parcialmente en tendida, é pensado que cada neurônio dispara impulsos elétricos de acordo com regras simples mais de mil vezes por segundo. Então o que nós temos é um computador interconectado capaz de talvez 1014 operações por segundo; por comparação, o supercomputador paralelo mais rápido do mundo, a máquina de teraflops 9200-Pentium Pro em Sandia National Labs, pode realizar 1012 operações por segundo. Contrariamente à c rença popular, m assa cinzenta não é apenas **hard-wired** para inteligência: ultrapassa silícioaté mesmo em poder computacional bruto. Mas isto não parece permanecer verdadeiro por muito tempo. A razão disso é a Lei do Moore, a qual, na sua formulação em 1990, atesta que a quantidade de informação armazenada em ch ips de silício cresce exponencialmente, dobrando mais ou menos a cada dois anos. A Lei de Moore acabará **to play out** conforme componentes de microchips alcançam a escala atômica e litografia convencional **to falter / falters**. Mas novas tecnologias radicais, tais como computadores ópticos, computadores de DNA, ou até mesmo computadores quânticos, poderiam **conceivably** usurpar o lugar do silício. Crescimento exponencial em poder computacional não pode continuar para sempre, mas pode continuar o suficiente para computadores - ao menos em poder de processamento - ultrapassarem cérebros humanos. Aos **prognosticators - prognosticadores** da inteligência artificial, a Lei de Moore é um **herald - marco** do crescimento exponencial. Mas exponenciais têm um lado **drearier** também. A população humana recentemente passou de seis milhões e está dobrando a mais ou menos cada 40 anos. Nesta taxa exponencial, se uma pessoa média pesa setenta kilogramas, então pelo ano 3750 a Terra inteira será composta de carne humana. Mas antes que você invista em desodorante, tenha em mente que a população irá parar de crescer muito antes disso - seja por causa de fome, doenças epidêmicas, aquecimento global, extinções massivas de espécies, ar não-respiravel ou, entrando no reino especulativo, controle de natalidade. Não é dificil **to fathom** por que o físico Albert Bartlett **asserted** "**the greatest shortcoming** da raça humana" ser "nossa inabilidade de entender a função exponencial." Ou por que Carl Sagan nos advertiu para "nunca subestimar uma exponencial." Em seu livro Billions & Billions, Sagan deu algumas consequências deprimentes do crescimento exponencial. Numa taxa de inflação de 5% ao ano, um dolar vale apenas trinta e sete cents depois de vinte anos. Se um núcleo de urânio emite dois nêutrons, ambos os quais colidirão com outros núcleos de urânio, causando esses núcleos a emitirem 2 nêutrons, e assim por diante - bem, mencionei holocausto nuclear como um final possivel para o crescimento populacional?
Exponenciais são familiar, relevant, e intimamente conectados ao mundo físico e aos medos e esperanças humanos. Usando sistemas notacionais que discutirei depois, nós podemos concisamente representar números que fazem dos exponenciais **picayune** por comparação, que subjetivamente excedam tanto quanto este exceda 9. Mas esses novos sistemas parecem ser mais **abstruse** que exponenciais. No seu artigo "On Number Numbness", Douglas Hofstadter direciona seus leitores ao precipício desses sistemas, mas então **avers**:
Se nós fôssemos continuar nossa dscussão apenas um zilissegundo a mais, nos encontraríamos **smack-dab** no meio da teoria de funções recursivas e complexidade algorítmica, e isso seria abstrato demais. Então vamos largar o tópico aqui mesmo.
Mas deixar o assunto é esquecer não apenas a competição, mas qualquer esperança de entender como paradi gmas mais fortes direciona a números **vaster - mais vastos**. E então nós desembarcamos no início do século vinte, quando uma escola de matemáticos chamada de formalistas visaram colocar toda a Matemática em uma base axiomática rigorosa. Uma pergunta-chave para os formalistas era o que a palavra "computavel" significa, isto é, como podemos afirmar se uma sequência de números pode ser listada por um procedimento mecânico e bem definido? Alguns matemáticos pensaram que "computavel" coincidia com uma noção técnica chamada **recursive primitive - "recursiva primitiva"**. Mas, em 1928, Wilhel, Ackermann os refutou construindo uma sequência de números que é claramente computavel, mas cresce rápido demais para ser **primitive recursive**. A ideia de Ackermann era de criar um processamento sem fim de operações aritméticas, cada uma mais poderosa que a outra. Primeiro vem a adição. Depois, a multiplicação, que podemos pensar como adição sucessiva: por exemplo, 5*3 significa 5 adicionado a si mesmo 5 vezes, ou 5+5+5 = 15. Em terceiro vem a exponenciação, a qual podemos pensar como multiplicação repetida. Em quarto vem... o quê? Bem, nós temos de inventar uma operação estranha nova para exponeniação repetida. O matemático Rudy Rucker a chama de "tetration". Por exemplo, "5 'tetrated' a 3" significa 5 elevado a sua própria potência 3 vezes, ou
, um número com 2,185 dígitos. Podemos ir além. Em quinto vem "tetration" repetida: devemos chamá-la de "pentation"? Em sexto vem "pentation" repetida: "hexation"? As operações continuam infinitamente, cada qual **standing on** seu predecessor para elevar ainda mais o firmamento dos números grandes. Se cada operação fosse um sabor de doces, então a sequência de Ackermann seria o pacote de amostra, misturando um número de cada sabor. Primeiro na sequência é 1+1, ou (não segure sua respiração) 2. Segundo é 2*2, ou 4. Terceiro é 3 elevado ao cubo, ou 27. Ei, esses números não são tão grandes!
Fee. Fi. Fo. Fum.
Quarto é 4 "tetrated" a 4, ou
, que tem 10154 dígitos. Se você está planejando escrever este número, melhor começar agora. Em quinto vem 5 "pentated" na quinta, ou 
, com "5 'pentated' na quarta" numerais na pilha. Este número é colossal demais para descrever em termos ordinários. E os números ficam apenas maiores a partir daqui.
Mantendo a sequência de Ackermann, podemos **to clobber** oponentes **unschooled** na competição do maior número. Mas precisamos ser cuidadosos, uma vez que há muitas definições da sequência de Ackermann, não todas idênticas. Dentro do limite de quinze segundos, aqui está o que eu poderia ter escrito para evitar ambiguidade:
A(111)-sequência de Ackermann -A(1)=1+1, A(2)=2*2, A(3)=33, etc
**Recondite** como parece, a sequência de Ackermann realmente tem algumas aplicações. Um problema numa área chamada teoria de Ramsey pede pela dimensão mínima de um hipercubo satisfazendo uma certa propriedade. A dimensão verdadeira pensa-se ser 6, mas a menor dimensão que qualquer um conseguiu provar é tão grande que só pode ser expressa usando a mesma "aritmética estranha" na qual se baseia a sequência de Ackermann. De fato, o Guinness Book of World Records uma vez listou esta dimensão como o maior número já usado em uma prova matemática (outro **contender para o título foi o número de Skewes, mais ou menos
, que aparece no estudo de como os números primos são distribuídos. O famoso matemático G. H. Hardy **quipped** que o número de Skewes era "o maior número que já tinha servido para algum propósito definido na Matemática."). Além disso,
"the largest number which has ever served any definite purpose in mathematics.") What’s more, Ackermann’s briskly-rising cavalcade performs an occasional cameo in computer science. For example, in the analysis of a data structure called ‘Union-Find,’ a term gets multiplied by the inverse of the Ackermann sequence—meaning, for each whole number X, the first number N such that the Nth Ackermann number is bigger than X. The inverse grows as slowly as Ackermann’s original sequence grows quickly; for all practical purposes, the inverse is at most 4.
"Computing," said Turing,
is normally done by writing certain symbols on paper. We may suppose this paper to be divided into squares like a child’s arithmetic book. In elementary arithmetic the 2-dimensional character of the paper is sometimes used. But such use is always avoidable, and I think it will be agreed that the two-dimensional character of paper is no essential of computation. I assume then that the computation is carried out on one-dimensional paper, on a tape divided into squares. Turing continued to explicate his machine using ingenious reasoning from first principles. The tape, said Turing, extends infinitely in both directions, since a theoretical machine ought not be constrained by physical limits on resources. Furthermore, there’s a symbol written on each square of the tape, like the ‘1’s and ‘0’s in a modern computer’s memory. But how are the symbols manipulated? Well, there’s a ‘tape head’ moving back and forth along the tape, examining one square at a time, writing and erasing symbols according to definite rules. The rules are the tape head’s program: change them, and you change what the tape head does.
Turing’s august insight was that we can program the tape head to carry out any computation. Turing machines can add, multiply, extract cube roots, sort, search, spell-check, parse, play Tic-Tac-Toe, list the Ackermann sequence. If we represented keyboard input, monitor output, and so forth as symbols on the tape, we could even run Windows on a Turing machine. But there’s a problem. Set a tape head loose on a sequence of symbols, and it might stop eventually, or it might run forever—like the fabled programmer who gets stuck in the shower because the instructions on the shampoo bottle read "lather, rinse, repeat." If the machine’s going to run forever, it’d be nice to know this in advance, so that we don’t spend an eternity waiting for it to finish. But how can we determine, in a finite amount of time, whether something will go on endlessly? If you bet a friend that your watch will never stop ticking, when could you declare victory? But maybe there’s some ingenious program that can examine other programs and tell us, infallibly, whether they’ll ever stop running. We just haven’t thought of it yet.
Nope. Turing proved that this problem, called the Halting Problem, is unsolvable by Turing machines. The proof is a beautiful example of self-reference. It formalizes an old argument about why you can never have perfect introspection: because if you could, then you could determine what you were going to do ten seconds from now, and then do something else. Turing imagined that there was a special machine that could solve the Halting Problem. Then he showed how we could have this machine analyze itself, in such a way that it has to halt if it runs forever, and run forever if it halts. Like a hound that finally catches its tail and devours itself, the mythical machine vanishes in a fury of contradiction. (That’s the sort of thing you don’t say in a research paper.)
His idea was simple. Just as we can classify words by how many letters they contain, we can classify Turing machines by how many rules they have in the tape head. Some machines have only one rule, others have two rules, still others have three rules, and so on. But for each fixed whole number N, just as there are only finitely many words with N letters, so too are there only finitely many machines with N rules. Among these machines, some halt and others run forever when started on a blank tape. Of the ones that halt, asked Rado, what’s the maximum number of steps that any machine takes before it halts? (Actually, Rado asked mainly about the maximum number of symbols any machine can write on the tape before halting. But the maximum number of steps, which Rado called S(n), has the same basic properties and is easier to reason about.)
Rado called this maximum the Nth "Busy Beaver" number. (Ah yes, the early 1960’s were a more innocent age.) He visualized each Turing machine as a beaver bustling busily along the tape, writing and erasing symbols. The challenge, then, is to find the busiest beaver with exactly N rules, albeit not an infinitely busy one. We can interpret this challenge as one of finding the "most complicated" computer program N bits long: the one that does the most amount of stuff, but not an infinite amount.
Now, suppose we knew the Nth Busy Beaver number, which we’ll call BB(N). Then we could decide whether any Turing machine with N rules halts on a blank tape. We’d just have to run the machine: if it halts, fine; but if it doesn’t halt within BB(N) steps, then we know it never will halt, since BB(N) is the maximum number of steps it could make before halting. Similarly, if you knew that all mortals died before age 200, then if Sally lived to be 200, you could conclude that Sally was immortal. So no Turing machine can list the Busy Beaver numbers—for if it could, it could solve the Halting Problem, which we already know is impossible.
But here’s a curious fact. Suppose we could name a number greater than the Nth Busy Beaver number BB(N). Call this number D for dam, since like a beaver dam, it’s a roof for the Busy Beaver below. With D in hand, computing BB(N) itself becomes easy: we just need to simulate all the Turing machines with N rules. The ones that haven’t halted within D steps—the ones that bash through the dam’s roof—never will halt. So we can list exactly which machines halt, and among these, the maximum number of steps that any machine takes before it halts is BB(N).
Conclusion? The sequence of Busy Beaver numbers, BB(1), BB(2), and so on, grows faster than any computable sequence. Faster than exponentials, stacked exponentials, the Ackermann sequence, you name it. Because if a Turing machine could compute a sequence that grows faster than Busy Beaver, then it could use that sequence to obtain the D‘s—the beaver dams. And with those D’s, it could list the Busy Beaver numbers, which (sound familiar?) we already know is impossible. The Busy Beaver sequence is non-computable, solely because it grows stupendously fast—too fast for any computer to keep up with it, even in principle.
This means that no computer program could list all the Busy Beavers one by one. It doesn’t mean that specific Busy Beavers need remain eternally unknowable. And in fact, pinning them down has been a computer science pastime ever since Rado published his article. It’s easy to verify that BB(1), the first Busy Beaver number, is 1. That’s because if a one-rule Turing machine doesn’t halt after the very first step, it’ll just keep moving along the tape endlessly. There’s no room for any more complex behavior. With two rules we can do more, and a little grunt work will ascertain that BB(2) is 6. Six steps. What about the third Busy Beaver? In 1965 Rado, together with Shen Lin, proved that BB(3) is 21. The task was an arduous one, requiring human analysis of many machines to prove that they don’t halt—since, remember, there’s no algorithm for listing the Busy Beaver numbers. Next, in 1983, Allan Brady proved that BB(4) is 107. Unimpressed so far? Well, as with the Ackermann sequence, don’t be fooled by the first few numbers.
In 1984, A.K. Dewdney devoted a Scientific American column to Busy Beavers, which inspired amateur mathematician George Uhing to build a special-purpose device for simulating Turing machines. The device, which cost Uhing less than $100, found a five-rule machine that runs for 2,133,492 steps before halting—establishing that BB(5) must be at least as high. Then, in 1989, Heiner Marxen and Jürgen Buntrock discovered that BB(5) is at least 47,176,870. To this day, BB(5) hasn’t been pinned down precisely, and it could turn out to be much higher still. As for BB(6), Marxen and Buntrock set another record in 1997 by proving that it’s at least 8,690,333,381,690,951. A formidable accomplishment, yet Marxen, Buntrock, and the other Busy Beaver hunters are merely wading along the shores of the unknowable. Humanity may never know the value of BB(6) for certain, let alone that of BB(7) or any higher number in the sequence.
Indeed, already the top five and six-rule contenders elude us: we can’t explain how they ‘work’ in human terms. If creativity imbues their design, it’s not because humans put it there. One way to understand this is that even small Turing machines can encode profound mathematical problems. Take Goldbach’s conjecture, that every even number 4 or higher is a sum of two prime numbers: 10=7+3, 18=13+5. The conjecture has resisted proof since 1742. Yet we could design a Turing machine with, oh, let’s say 100 rules, that tests each even number to see whether it’s a sum of two primes, and halts when and if it finds a counterexample to the conjecture. Then knowing BB(100), we could in principle run this machine for BB(100) steps, decide whether it halts, and thereby resolve Goldbach’s conjecture. We need not venture far in the sequence to enter the lair of basilisks.
But as Rado stressed, even if we can’t list the Busy Beaver numbers, they’re perfectly well-defined mathematically. If you ever challenge a friend to the biggest number contest, I suggest you write something like this:
BB(11111)—Busy Beaver shift #—1, 6, 21, etc If your friend doesn’t know about Turing machines or anything similar, but only about, say, Ackermann numbers, then you’ll win the contest. You’ll still win even if you grant your friend a handicap, and allow him the entire lifetime of the universe to write his number. The key to the biggest number contest is a potent paradigm, and Turing’s theory of computation is potent indeed.
Suppose we could endow a Turing machine with a magical ability to solve the Halting Problem. What would we get? We’d get a ‘super Turing machine’: one with abilities beyond those of any ordinary machine. But now, how hard is it to decide whether a super machine halts? Hmm. It turns out that not even super machines can solve this ‘super Halting Problem’, for the same reason that ordinary machines can’t solve the ordinary Halting Problem. To solve the Halting Problem for super machines, we’d need an even more powerful machine: a ‘super duper machine.’ And to solve the Halting Problem for super duper machines, we’d need a ‘super duper pooper machine.’ And so on endlessly. This infinite hierarchy of ever more powerful machines was formalized by the logician Stephen Kleene in 1943 (although he didn’t use the term ‘super duper pooper’).
Imagine a novel, which is imbedded in a longer novel, which itself is imbedded in an even longer novel, and so on ad infinitum. Within each novel, the characters can debate the literary merits of any of the sub-novels. But, by analogy with classes of machines that can’t analyze themselves, the characters can never critique the novel that they themselves are in. (This, I think, jibes with our ordinary experience of novels.) To fully understand some reality, we need to go outside of that reality. This is the essence of Kleene’s hierarchy: that to solve the Halting Problem for some class of machines, we need a yet more powerful class of machines.
And there’s no escape. Suppose a Turing machine had a magical ability to solve the Halting Problem, and the super Halting Problem, and the super duper Halting Problem, and the super duper pooper Halting Problem, and so on endlessly. Surely this would be the Queen of Turing machines? Not quite. As soon as we want to decide whether a ‘Queen of Turing machines’ halts, we need a still more powerful machine: an ‘Empress of Turing machines.’ And Kleene’s hierarchy continues.
But how’s this relevant to big numbers? Well, each level of Kleene’s hierarchy generates a faster-growing Busy Beaver sequence than do all the previous levels. Indeed, each level’s sequence grows so rapidly that it can only be computed by a higher level. For example, define BB2(N) to be the maximum number of steps a super machine with N rules can make before halting. If this super Busy Beaver sequence were computable by super machines, then those machines could solve the super Halting Problem, which we know is impossible. So the super Busy Beaver numbers grow too rapidly to be computed, even if we could compute the ordinary Busy Beaver numbers.
You might think that now, in the biggest-number contest, you could obliterate even an opponent who uses the Busy Beaver sequence by writing something like this:
BB2(11111). But not quite. The problem is that I’ve never seen these "higher-level Busy Beavers" defined anywhere, probably because, to people who know computability theory, they’re a fairly obvious extension of the ordinary Busy Beaver numbers. So our reasonable modern mathematician wouldn’t know what number you were naming. If you want to use higher-level Busy Beavers in the biggest number contest, here’s what I suggest. First, publish a paper formalizing the concept in some obscure, low-prestige journal. Then, during the contest, cite the paper on your index card.
To exceed higher-level Busy Beavers, we’d presumably need some new computational model surpassing even Turing machines. I can’t imagine what such a model would look like. Yet somehow I doubt that the story of notational systems for big numbers is over. Perhaps someday humans will be able concisely to name numbers that make Busy Beaver 100 seem as puerile and amusingly small as our nobleman’s eighty-three. Or if we’ll never name such numbers, perhaps other civilizations will. Is a biggest number contest afoot throughout the galaxy?
The biggest whole number nameable with 1,000 characters of English text Surely this number exists. Using 1,000 characters, we can name only finitely many numbers, and among these numbers there has to be a biggest. And yet we’ve made no reference to how the number’s named. The English text could invoke Ackermann numbers, or Busy Beavers, or higher-level Busy Beavers, or even some yet more sweeping concept that nobody’s thought of yet. So unless our opponent uses the same ploy, we’ve got him licked. What a brilliant idea! Why didn’t we think of this earlier?
Unfortunately it doesn’t work. We might as well have written
One plus the biggest whole number nameable with 1,000 characters of English text This number takes at least 1,001 characters to name. Yet we’ve just named it with only 80 characters! Like a snake that swallows itself whole, our colossal number dissolves in a tumult of contradiction. What gives?
The paradox I’ve just described was first published by Bertrand Russell, who attributed it to a librarian named G. G. Berry. The Berry Paradox arises not from mathematics, but from the ambiguity inherent in the English language. There’s no surefire way to convert an English phrase into the number it names (or to decide whether it names a number at all), which is why I invoked a "reasonable modern mathematician" in the rules for the biggest number contest. To circumvent the Berry Paradox, we need to name numbers using a precise, mathematical notational system, such as Turing machines—which is exactly the idea behind the Busy Beaver sequence. So in short, there’s no wily language trick by which to surpass Archimedes, Ackermann, Turing, and Rado, no royal road to big numbers.
You might also wonder why we can’t use infinity in the contest. The answer is, for the same reason why we can’t use a rocket car in a bike race. Infinity is fascinating and elegant, but it’s not a whole number. Nor can we ‘subtract from infinity’ to yield a whole number. Infinity minus 17 is still infinity, whereas infinity minus infinity is undefined: it could be 0, 38, or even infinity again. Actually I should speak of infinities, plural. For in the late nineteenth century, Georg Cantor proved that there are different levels of infinity: for example, the infinity of points on a line is greater than the infinity of whole numbers. What’s more, just as there’s no biggest number, so too is there no biggest infinity. But the quest for big infinities is more abstruse than the quest for big numbers. And it involves, not a succession of paradigms, but essentially one: Cantor’s.
Imagine trying to explain the Turing machine to Archimedes. The genius of Syracuse listens patiently as you discuss the papyrus tape extending infinitely in both directions, the time steps, states, input and output sequences. At last he explodes.
"Foolishness!" he declares (or the ancient Greek equivalent). "All you’ve given me is an elaborate definition, with no value outside of itself."
How do you respond? Archimedes has never heard of computers, those cantankerous devices that, twenty-three centuries from his time, will transact the world’s affairs. So you can’t claim practical application. Nor can you appeal to Hilbert and the formalist program, since Archimedes hasn’t heard of those either. But then it hits you: the Busy Beaver sequence. You define the sequence for Archimedes, convince him that BB(1000) is more than his 1063 grains of sand filling the universe, more even than 1063 raised to its own power 1063 times. You defy him to name a bigger number without invoking Turing machines or some equivalent. And as he ponders this challenge, the power of the Turing machine concept dawns on him. Though his intuition may never apprehend the Busy Beaver numbers, his reason compels him to acknowledge their immensity. Big numbers have a way of imbuing abstract notions with reality.
Indeed, one could define science as reason’s attempt to compensate for our inability to perceive big numbers. If we could run at 280,000,000 meters per second, there’d be no need for a special theory of relativity: it’d be obvious to everyone that the faster we go, the heavier and squatter we get, and the faster time elapses in the rest of the world. If we could live for 70,000,000 years, there’d be no theory of evolution, and certainly no creationism: we could watch speciation and adaptation with our eyes, instead of painstakingly reconstructing events from fossils and DNA. If we could bake bread at 20,000,000 degrees Kelvin, nuclear fusion would be not the esoteric domain of physicists but ordinary household knowledge. But we can’t do any of these things, and so we have science, to deduce about the gargantuan what we, with our infinitesimal faculties, will never sense. If people fear big numbers, is it any wonder that they fear science as well and turn for solace to the comforting smallness of mysticism?
But do people fear big numbers? Certainly they do. I’ve met people who don’t know the difference between a million and a billion, and don’t care. We play a lottery with ‘six ways to win!,’ overlooking the twenty million ways to lose. We yawn at six billion tons of carbon dioxide released into the atmosphere each year, and speak of ‘sustainable development’ in the jaws of exponential growth. Such cases, it seems to me, transcend arithmetical ignorance and represent a basic unwillingness to grapple with the immense.
Whence the cowering before big numbers, then? Does it have a biological origin? In 1999, a group led by neuropsychologist Stanislas Dehaene reported evidence in Science that two separate brain systems contribute to mathematical thinking. The group trained Russian-English bilinguals to solve a set of problems, including two-digit addition, base-eight addition, cube roots, and logarithms. Some subjects were trained in Russian, others in English. When the subjects were then asked to solve problems approximately—to choose the closer of two estimates—they performed equally well in both languages. But when asked to solve problems exactly, they performed better in the language of their training. What’s more, brain-imaging evidence showed that the subjects’ parietal lobes, involved in spatial reasoning, were more active during approximation problems; while the left inferior frontal lobes, involved in verbal reasoning, were more active during exact calculation problems. Studies of patients with brain lesions paint the same picture: those with parietal lesions sometimes can’t decide whether 9 is closer to 10 or to 5, but remember the multiplication table; whereas those with left-hemispheric lesions sometimes can’t decide whether 2+2 is 3 or 4, but know that the answer is closer to 3 than to 9. Dehaene et al. conjecture that humans represent numbers in two ways. For approximate reckoning we use a ‘mental number line,’ which evolved long ago and which we likely share with other animals. But for exact computation we use numerical symbols, which evolved recently and which, being language-dependent, are unique to humans. This hypothesis neatly explains the experiment’s findings: the reason subjects performed better in the language of their training for exact computation but not for approximation problems is that the former call upon the verbally-oriented left inferior frontal lobes, and the latter upon the spatially-oriented parietal lobes.
If Dehaene et al.’s hypothesis is correct, then which representation do we use for big numbers? Surely the symbolic one—for nobody’s mental number line could be long enough to contain, 5 pentated to the 5, or BB(1000). And here, I suspect, is the problem. When thinking about 3, 4, or 7, we’re guided by our spatial intuition, honed over millions of years of perceiving 3 gazelles, 4 mates, 7 members of a hostile clan. But when thinking about BB(1000), we have only language, that evolutionary neophyte, to rely upon. The usual neural pathways for representing numbers lead to dead ends. And this, perhaps, is why people are afraid of big numbers.
Could early intervention mitigate our big number phobia? What if second-grade math teachers took an hour-long hiatus from stultifying busywork to ask their students, "How do you name really, really big numbers?" And then told them about exponentials and stacked exponentials, tetration and the Ackermann sequence, maybe even Busy Beavers: a cornucopia of numbers vaster than any they’d ever conceived, and ideas stretching the bounds of their imaginations.
Who can name the bigger number? Whoever has the deeper paradigm. Are you ready? Get set. Go.
References Petr Beckmann, A History of Pi, Golem Press, 1971.
Allan H. Brady, "The Determination of the Value of Rado’s Noncomputable Function Sigma(k) for Four-State Turing Machines," Mathematics of Computation, vol. 40, no. 162, April 1983, pp 647- 665.
Gregory J. Chaitin, "The Berry Paradox," Complexity, vol. 1, no. 1, 1995, pp. 26- 30. At http://www.umcs.maine.edu/~chaitin/unm2.html.
A.K. Dewdney, The New Turing Omnibus: 66 Excursions in Computer Science, W.H. Freeman, 1993.
S. Dehaene and E. Spelke and P. Pinel and R. Stanescu and S. Tsivkin, "Sources of Mathematical Thinking: Behavioral and Brain-Imaging Evidence," Science, vol. 284, no. 5416, May 7, 1999, pp. 970- 974.
Douglas Hofstadter, Metamagical Themas: Questing for the Essence of Mind and Pattern, Basic Books, 1985. Chapter 6, "On Number Numbness," pp. 115- 135.
Robert Kanigel, The Man Who Knew Infinity: A Life of the Genius Ramanujan, Washington Square Press, 1991.
Stephen C. Kleene, "Recursive predicates and quantifiers," Transactions of the American Mathematical Society, vol. 53, 1943, pp. 41- 74.
Donald E. Knuth, Selected Papers on Computer Science, CSLI Publications, 1996. Chapter 2, "Mathematics and Computer Science: Coping with Finiteness," pp. 31- 57.
Dexter C. Kozen, Automata and Computability, Springer-Verlag, 1997.
———, The Design and Analysis of Algorithms, Springer-Verlag, 1991.
Shen Lin and Tibor Rado, "Computer studies of Turing machine problems," Journal of the Association for Computing Machinery, vol. 12, no. 2, April 1965, pp. 196- 212.
Heiner Marxen, Busy Beaver, at http://www.drb.insel.de/~heiner/BB/.
——— and Jürgen Buntrock, "Attacking the Busy Beaver 5," Bulletin of the European Association for Theoretical Computer Science, no. 40, February 1990, pp. 247- 251.
Tibor Rado, "On Non-Computable Functions," Bell System Technical Journal, vol. XLI, no. 2, May 1962, pp. 877- 884.
Rudy Rucker, Infinity and the Mind, Princeton University Press, 1995.
Carl Sagan, Billions & Billions, Random House, 1997.
Michael Somos, "Busy Beaver Turing Machine." At http://grail.cba.csuohio.edu/~somos/bb.html.
Alan Turing, "On computable numbers, with an application to the Entscheidungsproblem," Proceedings of the London Mathematical Society, Series 2, vol. 42, pp. 230- 265, 1936. Reprinted in Martin Davis (ed.), The Undecidable, Raven, 1965.
Ilan Vardi, "Archimedes, the Sand Reckoner," at http://www.ihes.fr/~ilan/sand_reckoner.ps.
Eric W. Weisstein, CRC Concise Encyclopedia of Mathematics, CRC Press, 1999. Entry on "Large Number" at http://www.treasure-troves.com/math/LargeNumber.html.
by Scott Aaronson
[Author's blog]
Em uma antiga piada, dois nobres **vie** nomear/representar* o maior número. O primeiro, após ruminar por horas, triumfantemente anuncia "Oitenta e três!". O segundo, poderosamente impressionado, responde "Você venceu."
Uma competição do número maior é claramente sem sentido quando os participantes atuam por turnos alternados. Mas o que acontece se os competidores escrevem seus números simultaneamente, nenhum **aware of** outro? Para introduzir uma conversa sobre "Big Numbers," eu convidei dois voluntários para tentar exartamente isto. Digo a eles as regras:
Vocês têm quinze segundos. Usando notação matemática padrão, palavras em Inglês, ou ambos, representem um único número por extenso - não uma infinidade - em um ** index card / cartão-ficha** em branco. Sejam precisos o suficiente para qualquer matemático moderno determinar exatamente que número vocês representaram consultando apenas seu cartão e, se necessário, literatura publicada.
Então os competidores não podem dizer "o número de grãos de areia do Saara," porque areia sai e entra no Saara regularmente. Também não podem dizer "o número do meu oponente mais um" ou "o maior número que qualquer pessoa já tenha pensado mais um" - novamente, estes número são mal definidos, dado o que nosso matemático razoavel tem disponivel. Dentro das regras, o competidor que representasse o maior número vence. Estão prontos? Preparar. Vão.
Os resultados da competição nunca foram como eu esperava. Uma vez, um garoto do sétimo ano encheu seu cartão com uma **string** de 9's sucessivos. Como muitos outros **big-number tyros**, ele procurou maximizar seu número enchendo um 9 em todo espaço disponivel. Se ele tivesse escolhido escrever 1's ao invés do 9 curvilíneo, seu número poderia ter sido milhões de vezes maior. Ele ainda teria sido **decimated**, no entanto, pela garota que ele estava competindo contra, que escreveu uma **string** de 9's seguido pelo sobrescrito 999. A-ha! um exponencial: um número multiplicado por si mesmo 999 vezes. Notando essa inovação, declarei a vitória da garota sem me importar contar os 9's nos cartões.
E, mesmo que o número da garota tivesse sido muito maior, seria maior ainda se ela tivesse **stacked** o exponencial mais do que uma vez. Take
Tais paradigmas são raridades históricas. Achamos **a flurry** na anrtiguidade, **another flurry** no século vinte, e não muito entre esses dois períodos. Mas, quando um novo modo para expressar grandes números concisamente emerge de fato, é sempre como produto conjunto de uma grande revolução científica: matemática sistematizada, lógica formal, ciência da computação. **Revolutions this momentous**, como qualquer **Kuhnian** diria a você, apenas ocorrem sob determinadas condições sociais. Assim é a história dos números grandes uma história do progresso humano.
E dentro disso permanece um paralelo com outra história matemática. No seu livro **remarkable** e **underappreciated** A History of Pi, Petr Beckmann argumenta qu e a razão da circunferência para o diâmetro é "um espelho **quaint little** da história do homem." Nas raras sociedades onde ciência e razão encontraram refúgio - a antiga Atenas de **Anaxagoras** e **Hippias**, a Alexandria de **Erastostenes** e Euclides, a Inglaterra do século XVII de Nerwton e Wallis - matemáticos fizeram saltos tremendos no cálculo de pi. Em Roma e na Europa medieval, em contraste, o conhecimento do pi estagnou. Aproximações cruas como os 25/8 dos babilônios **held sway**.
Este mesmo padrão permanece, eu acho, para números grandes. Curiosidade e **openness lead to fascination** com números grandes, e para **the buoyant view** que nenhuma quantidade, seja o número de estrelas na galáxia ou o número de de mãos de bridge possíveis, é imenso demais para a mente enumerar. **Conversely**, ignorância e irracionalidade levaram ao fatalismo sobre números grandes. O historiador Ilan Vardi cita a palavra grega antiga 'yammkosioi,' ou areia-entos, coloquialmente significando um zilhão; assim como uma passagem da Olympic Ode II, **asserting** que "areia escapa da contagem."
Mas a areia não escapa da contagem, como Arquimedes reconheceu no século terceiro AC. Aqui está como ele iniciou The Sand-Reckoner, algo como um artigo de ciência pop endereçado ao rei de **Siracusa**:
(...) Há alguns (...) que pensam que o número de grãos de areia é infinito **in multitude** (...) de novo há alguns que, sem levar em conta como inifnitos, ainda pensam que nenhum número foi dado que seja grande o suficiente para exceder essa **multitude**(...) Mas tentarei mostrar a você [números que] excedem não apenas o número de massa de areia igual em magnitude ao de terra (...), mas também uma massa igual em magnitude ao universo.
Assim Arquimedes procedeu para mostrar, essencialmente usando o termo grego antigo miríade, significando dez mil, como uma base para exponenciais. Adotando um modelo comológico **prescient** de **Aristarchus**, no qual a "esfera de cinco estrelas" é vastamente maior do que a esfera n a qual a Terra orbita ao redor do Sol, Arquimedes obteve um limite superior de 1063para o número de grãos de areia necessários para preencher o universo (supostamente 1063 é o maior número com um nome americano padrão lexicográfico: vingintillion. Mas o **staid** vingintillion manteve **vigil lest/last it be encroached** sob o mais **whimsically-named** googol, ou 10100, e googolplex, ou
Considere, por exemplo, a manjada lenda do Grão-vizir na Pérsia que inven tou o xadrez. O Rei, conforme diz a lenda, estava em deleite por causa do novo jogo e convidou o Vizir para **to name** sua própria recompensa. O Vizir respondeu que. sendo um homem modesto, desejava apenas um grão de trigo na primeira casa do tabuleiro de xadrez, dois grãos na segunda, quatro na terceira e assim por diante, com o dobro da quantidade de grãos da casa anterior na atual. O Rei **innumerate** concordou sem se dar conta que o total de grãos em todas as 64 casas seria de 264-1, ou 18.6 quintilhões - o equivalente à produção atual de trigo por 150 anos.
De maneira adequada, este crescimemnto exponencial é o que faz o próprio xadrez tão dificil. Há apenas 35 escolhas legalmente aceitas para cada movimento no xadrez, mas as escolhas multiplicam exponencialmente para **to yield** mais de 1050movimentos possíveis - movimentos demais para até mesmo um computador procurar exaustivamente. Isto é o que levou até 1997 para um computador, Deep Blue, derrotar o campeão mundial humano de xadrez. E em Go, que tem um tabuleiro de 19x19 casas e mais de 10150posições possíveis, até mesmo um humano amador pode **to rout** o programa de computador na posição mais alta do ranking. Crescimento exponencial **to plague** computadores em outros **guises** também. O problema do caixeiro viajante pede a rota mais curta conectando um conjunto de cidades, dadas as distâncias entre cada par de cidades. **The rub** é que o número de rotas possíveis cresce exponencialmente com o número de cidades. Quando há, digamos, 100 cidades, há por volta de 10158rotas possíveis e, embora vários atalhos sejam possíveis, nenhum algoritmo para computador é fundamentalmente melhor do que checar rotas uma a uma (método de força bruta). O problema do caixeiro viajante pertence a uma classe chamada NP-completa, a qual inclui centenas de outros problemas de interesse prático (NP representa o termo técnico "Tempo Polinomial Não-Determinístico"). É sabido que, se há algum algoritmo eficiente para algum problema NP-completo, então há algoritmos eficientes para todos eles. Aqui "eficiente" significa que, usando uma quantidade de tempo proporcional de, no máximo, o tamanho do problema elevado a algum expoente fixo - por exemplo, o núm ero de cidades ao cubo - . É conjecturado, no entantom que nenhum algoritmo para problemas NP-completos exista. Provando esta conjectura, chamada P = NP, tem sido um grande problema não-solucionado da Ciência da Computação por trinta anos.
Embora computadores provavelmente nunca resolvam problemas NP-completos eficientemente , há mais esperança para outro **grail - cálice/cálice sagrado** da Ciência da Computação: replicar a inteligência humana. O cérebro humano tem aproximadamente um bi lhão de neurônios ligados por cem trilhões de sinapses. E, apesar da função de um único neurônio ser apenas parcialmente en tendida, é pensado que cada neurônio dispara impulsos elétricos de acordo com regras simples mais de mil vezes por segundo. Então o que nós temos é um computador interconectado capaz de talvez 1014 operações por segundo; por comparação, o supercomputador paralelo mais rápido do mundo, a máquina de teraflops 9200-Pentium Pro em Sandia National Labs, pode realizar 1012 operações por segundo. Contrariamente à c rença popular, m assa cinzenta não é apenas **hard-wired** para inteligência: ultrapassa silícioaté mesmo em poder computacional bruto. Mas isto não parece permanecer verdadeiro por muito tempo. A razão disso é a Lei do Moore, a qual, na sua formulação em 1990, atesta que a quantidade de informação armazenada em ch ips de silício cresce exponencialmente, dobrando mais ou menos a cada dois anos. A Lei de Moore acabará **to play out** conforme componentes de microchips alcançam a escala atômica e litografia convencional **to falter / falters**. Mas novas tecnologias radicais, tais como computadores ópticos, computadores de DNA, ou até mesmo computadores quânticos, poderiam **conceivably** usurpar o lugar do silício. Crescimento exponencial em poder computacional não pode continuar para sempre, mas pode continuar o suficiente para computadores - ao menos em poder de processamento - ultrapassarem cérebros humanos. Aos **prognosticators - prognosticadores** da inteligência artificial, a Lei de Moore é um **herald - marco** do crescimento exponencial. Mas exponenciais têm um lado **drearier** também. A população humana recentemente passou de seis milhões e está dobrando a mais ou menos cada 40 anos. Nesta taxa exponencial, se uma pessoa média pesa setenta kilogramas, então pelo ano 3750 a Terra inteira será composta de carne humana. Mas antes que você invista em desodorante, tenha em mente que a população irá parar de crescer muito antes disso - seja por causa de fome, doenças epidêmicas, aquecimento global, extinções massivas de espécies, ar não-respiravel ou, entrando no reino especulativo, controle de natalidade. Não é dificil **to fathom** por que o físico Albert Bartlett **asserted** "**the greatest shortcoming** da raça humana" ser "nossa inabilidade de entender a função exponencial." Ou por que Carl Sagan nos advertiu para "nunca subestimar uma exponencial." Em seu livro Billions & Billions, Sagan deu algumas consequências deprimentes do crescimento exponencial. Numa taxa de inflação de 5% ao ano, um dolar vale apenas trinta e sete cents depois de vinte anos. Se um núcleo de urânio emite dois nêutrons, ambos os quais colidirão com outros núcleos de urânio, causando esses núcleos a emitirem 2 nêutrons, e assim por diante - bem, mencionei holocausto nuclear como um final possivel para o crescimento populacional?
Exponenciais são familiar, relevant, e intimamente conectados ao mundo físico e aos medos e esperanças humanos. Usando sistemas notacionais que discutirei depois, nós podemos concisamente representar números que fazem dos exponenciais **picayune** por comparação, que subjetivamente excedam
Se nós fôssemos continuar nossa dscussão apenas um zilissegundo a mais, nos encontraríamos **smack-dab** no meio da teoria de funções recursivas e complexidade algorítmica, e isso seria abstrato demais. Então vamos largar o tópico aqui mesmo.
Mas deixar o assunto é esquecer não apenas a competição, mas qualquer esperança de entender como paradi gmas mais fortes direciona a números **vaster - mais vastos**. E então nós desembarcamos no início do século vinte, quando uma escola de matemáticos chamada de formalistas visaram colocar toda a Matemática em uma base axiomática rigorosa. Uma pergunta-chave para os formalistas era o que a palavra "computavel" significa, isto é, como podemos afirmar se uma sequência de números pode ser listada por um procedimento mecânico e bem definido? Alguns matemáticos pensaram que "computavel" coincidia com uma noção técnica chamada **recursive primitive - "recursiva primitiva"**. Mas, em 1928, Wilhel, Ackermann os refutou construindo uma sequência de números que é claramente computavel, mas cresce rápido demais para ser **primitive recursive**. A ideia de Ackermann era de criar um processamento sem fim de operações aritméticas, cada uma mais poderosa que a outra. Primeiro vem a adição. Depois, a multiplicação, que podemos pensar como adição sucessiva: por exemplo, 5*3 significa 5 adicionado a si mesmo 5 vezes, ou 5+5+5 = 15. Em terceiro vem a exponenciação, a qual podemos pensar como multiplicação repetida. Em quarto vem... o quê? Bem, nós temos de inventar uma operação estranha nova para exponeniação repetida. O matemático Rudy Rucker a chama de "tetration". Por exemplo, "5 'tetrated' a 3" significa 5 elevado a sua própria potência 3 vezes, ou
Fee. Fi. Fo. Fum.
Quarto é 4 "tetrated" a 4, ou
Mantendo a sequência de Ackermann, podemos **to clobber** oponentes **unschooled** na competição do maior número. Mas precisamos ser cuidadosos, uma vez que há muitas definições da sequência de Ackermann, não todas idênticas. Dentro do limite de quinze segundos, aqui está o que eu poderia ter escrito para evitar ambiguidade:
A(111)-sequência de Ackermann -A(1)=1+1, A(2)=2*2, A(3)=33, etc
**Recondite** como parece, a sequência de Ackermann realmente tem algumas aplicações. Um problema numa área chamada teoria de Ramsey pede pela dimensão mínima de um hipercubo satisfazendo uma certa propriedade. A dimensão verdadeira pensa-se ser 6, mas a menor dimensão que qualquer um conseguiu provar é tão grande que só pode ser expressa usando a mesma "aritmética estranha" na qual se baseia a sequência de Ackermann. De fato, o Guinness Book of World Records uma vez listou esta dimensão como o maior número já usado em uma prova matemática (outro **contender para o título foi o número de Skewes, mais ou menos
"the largest number which has ever served any definite purpose in mathematics.") What’s more, Ackermann’s briskly-rising cavalcade performs an occasional cameo in computer science. For example, in the analysis of a data structure called ‘Union-Find,’ a term gets multiplied by the inverse of the Ackermann sequence—meaning, for each whole number X, the first number N such that the Nth Ackermann number is bigger than X. The inverse grows as slowly as Ackermann’s original sequence grows quickly; for all practical purposes, the inverse is at most 4.
¨
Ackermann numbers are pretty big, but they’re not yet big enough. The quest for still bigger numbers takes us back to the formalists. After Ackermann demonstrated that ‘primitive recursive’ isn’t what we mean by ‘computable,’ the question still stood: what do we mean by ‘computable’? In 1936, Alonzo Church and Alan Turing independently answered this question. While Church answered using a logical formalism called the lambda calculus, Turing answered using an idealized computing machine—the Turing machine—that, in essence, is equivalent to every Compaq, Dell, Macintosh, and Cray in the modern world. Turing’s paper describing his machine, "On Computable Numbers," is rightly celebrated as the founding document of computer science."Computing," said Turing,
Turing’s august insight was that we can program the tape head to carry out any computation. Turing machines can add, multiply, extract cube roots, sort, search, spell-check, parse, play Tic-Tac-Toe, list the Ackermann sequence. If we represented keyboard input, monitor output, and so forth as symbols on the tape, we could even run Windows on a Turing machine. But there’s a problem. Set a tape head loose on a sequence of symbols, and it might stop eventually, or it might run forever—like the fabled programmer who gets stuck in the shower because the instructions on the shampoo bottle read "lather, rinse, repeat." If the machine’s going to run forever, it’d be nice to know this in advance, so that we don’t spend an eternity waiting for it to finish. But how can we determine, in a finite amount of time, whether something will go on endlessly? If you bet a friend that your watch will never stop ticking, when could you declare victory? But maybe there’s some ingenious program that can examine other programs and tell us, infallibly, whether they’ll ever stop running. We just haven’t thought of it yet.
Nope. Turing proved that this problem, called the Halting Problem, is unsolvable by Turing machines. The proof is a beautiful example of self-reference. It formalizes an old argument about why you can never have perfect introspection: because if you could, then you could determine what you were going to do ten seconds from now, and then do something else. Turing imagined that there was a special machine that could solve the Halting Problem. Then he showed how we could have this machine analyze itself, in such a way that it has to halt if it runs forever, and run forever if it halts. Like a hound that finally catches its tail and devours itself, the mythical machine vanishes in a fury of contradiction. (That’s the sort of thing you don’t say in a research paper.)
¨
"Very nice," you say (or perhaps you say, "not nice at all"). "But what does all this have to do with big numbers?" Aha! The connection wasn’t published until May of 1962. Then, in the Bell System Technical Journal, nestled between pragmatically-minded papers on "Multiport Structures" and "Waveguide Pressure Seals," appeared the modestly titled "On Non-Computable Functions" by Tibor Rado. In this paper, Rado introduced the biggest numbers anyone had ever imagined. His idea was simple. Just as we can classify words by how many letters they contain, we can classify Turing machines by how many rules they have in the tape head. Some machines have only one rule, others have two rules, still others have three rules, and so on. But for each fixed whole number N, just as there are only finitely many words with N letters, so too are there only finitely many machines with N rules. Among these machines, some halt and others run forever when started on a blank tape. Of the ones that halt, asked Rado, what’s the maximum number of steps that any machine takes before it halts? (Actually, Rado asked mainly about the maximum number of symbols any machine can write on the tape before halting. But the maximum number of steps, which Rado called S(n), has the same basic properties and is easier to reason about.)
Rado called this maximum the Nth "Busy Beaver" number. (Ah yes, the early 1960’s were a more innocent age.) He visualized each Turing machine as a beaver bustling busily along the tape, writing and erasing symbols. The challenge, then, is to find the busiest beaver with exactly N rules, albeit not an infinitely busy one. We can interpret this challenge as one of finding the "most complicated" computer program N bits long: the one that does the most amount of stuff, but not an infinite amount.
Now, suppose we knew the Nth Busy Beaver number, which we’ll call BB(N). Then we could decide whether any Turing machine with N rules halts on a blank tape. We’d just have to run the machine: if it halts, fine; but if it doesn’t halt within BB(N) steps, then we know it never will halt, since BB(N) is the maximum number of steps it could make before halting. Similarly, if you knew that all mortals died before age 200, then if Sally lived to be 200, you could conclude that Sally was immortal. So no Turing machine can list the Busy Beaver numbers—for if it could, it could solve the Halting Problem, which we already know is impossible.
But here’s a curious fact. Suppose we could name a number greater than the Nth Busy Beaver number BB(N). Call this number D for dam, since like a beaver dam, it’s a roof for the Busy Beaver below. With D in hand, computing BB(N) itself becomes easy: we just need to simulate all the Turing machines with N rules. The ones that haven’t halted within D steps—the ones that bash through the dam’s roof—never will halt. So we can list exactly which machines halt, and among these, the maximum number of steps that any machine takes before it halts is BB(N).
Conclusion? The sequence of Busy Beaver numbers, BB(1), BB(2), and so on, grows faster than any computable sequence. Faster than exponentials, stacked exponentials, the Ackermann sequence, you name it. Because if a Turing machine could compute a sequence that grows faster than Busy Beaver, then it could use that sequence to obtain the D‘s—the beaver dams. And with those D’s, it could list the Busy Beaver numbers, which (sound familiar?) we already know is impossible. The Busy Beaver sequence is non-computable, solely because it grows stupendously fast—too fast for any computer to keep up with it, even in principle.
This means that no computer program could list all the Busy Beavers one by one. It doesn’t mean that specific Busy Beavers need remain eternally unknowable. And in fact, pinning them down has been a computer science pastime ever since Rado published his article. It’s easy to verify that BB(1), the first Busy Beaver number, is 1. That’s because if a one-rule Turing machine doesn’t halt after the very first step, it’ll just keep moving along the tape endlessly. There’s no room for any more complex behavior. With two rules we can do more, and a little grunt work will ascertain that BB(2) is 6. Six steps. What about the third Busy Beaver? In 1965 Rado, together with Shen Lin, proved that BB(3) is 21. The task was an arduous one, requiring human analysis of many machines to prove that they don’t halt—since, remember, there’s no algorithm for listing the Busy Beaver numbers. Next, in 1983, Allan Brady proved that BB(4) is 107. Unimpressed so far? Well, as with the Ackermann sequence, don’t be fooled by the first few numbers.
In 1984, A.K. Dewdney devoted a Scientific American column to Busy Beavers, which inspired amateur mathematician George Uhing to build a special-purpose device for simulating Turing machines. The device, which cost Uhing less than $100, found a five-rule machine that runs for 2,133,492 steps before halting—establishing that BB(5) must be at least as high. Then, in 1989, Heiner Marxen and Jürgen Buntrock discovered that BB(5) is at least 47,176,870. To this day, BB(5) hasn’t been pinned down precisely, and it could turn out to be much higher still. As for BB(6), Marxen and Buntrock set another record in 1997 by proving that it’s at least 8,690,333,381,690,951. A formidable accomplishment, yet Marxen, Buntrock, and the other Busy Beaver hunters are merely wading along the shores of the unknowable. Humanity may never know the value of BB(6) for certain, let alone that of BB(7) or any higher number in the sequence.
Indeed, already the top five and six-rule contenders elude us: we can’t explain how they ‘work’ in human terms. If creativity imbues their design, it’s not because humans put it there. One way to understand this is that even small Turing machines can encode profound mathematical problems. Take Goldbach’s conjecture, that every even number 4 or higher is a sum of two prime numbers: 10=7+3, 18=13+5. The conjecture has resisted proof since 1742. Yet we could design a Turing machine with, oh, let’s say 100 rules, that tests each even number to see whether it’s a sum of two primes, and halts when and if it finds a counterexample to the conjecture. Then knowing BB(100), we could in principle run this machine for BB(100) steps, decide whether it halts, and thereby resolve Goldbach’s conjecture. We need not venture far in the sequence to enter the lair of basilisks.
But as Rado stressed, even if we can’t list the Busy Beaver numbers, they’re perfectly well-defined mathematically. If you ever challenge a friend to the biggest number contest, I suggest you write something like this:
BB(11111)—Busy Beaver shift #—1, 6, 21, etc If your friend doesn’t know about Turing machines or anything similar, but only about, say, Ackermann numbers, then you’ll win the contest. You’ll still win even if you grant your friend a handicap, and allow him the entire lifetime of the universe to write his number. The key to the biggest number contest is a potent paradigm, and Turing’s theory of computation is potent indeed.
¨
But what if your friend knows about Turing machines as well? Is there a notational system for big numbers more powerful than even Busy Beavers?Suppose we could endow a Turing machine with a magical ability to solve the Halting Problem. What would we get? We’d get a ‘super Turing machine’: one with abilities beyond those of any ordinary machine. But now, how hard is it to decide whether a super machine halts? Hmm. It turns out that not even super machines can solve this ‘super Halting Problem’, for the same reason that ordinary machines can’t solve the ordinary Halting Problem. To solve the Halting Problem for super machines, we’d need an even more powerful machine: a ‘super duper machine.’ And to solve the Halting Problem for super duper machines, we’d need a ‘super duper pooper machine.’ And so on endlessly. This infinite hierarchy of ever more powerful machines was formalized by the logician Stephen Kleene in 1943 (although he didn’t use the term ‘super duper pooper’).
Imagine a novel, which is imbedded in a longer novel, which itself is imbedded in an even longer novel, and so on ad infinitum. Within each novel, the characters can debate the literary merits of any of the sub-novels. But, by analogy with classes of machines that can’t analyze themselves, the characters can never critique the novel that they themselves are in. (This, I think, jibes with our ordinary experience of novels.) To fully understand some reality, we need to go outside of that reality. This is the essence of Kleene’s hierarchy: that to solve the Halting Problem for some class of machines, we need a yet more powerful class of machines.
And there’s no escape. Suppose a Turing machine had a magical ability to solve the Halting Problem, and the super Halting Problem, and the super duper Halting Problem, and the super duper pooper Halting Problem, and so on endlessly. Surely this would be the Queen of Turing machines? Not quite. As soon as we want to decide whether a ‘Queen of Turing machines’ halts, we need a still more powerful machine: an ‘Empress of Turing machines.’ And Kleene’s hierarchy continues.
But how’s this relevant to big numbers? Well, each level of Kleene’s hierarchy generates a faster-growing Busy Beaver sequence than do all the previous levels. Indeed, each level’s sequence grows so rapidly that it can only be computed by a higher level. For example, define BB2(N) to be the maximum number of steps a super machine with N rules can make before halting. If this super Busy Beaver sequence were computable by super machines, then those machines could solve the super Halting Problem, which we know is impossible. So the super Busy Beaver numbers grow too rapidly to be computed, even if we could compute the ordinary Busy Beaver numbers.
You might think that now, in the biggest-number contest, you could obliterate even an opponent who uses the Busy Beaver sequence by writing something like this:
BB2(11111). But not quite. The problem is that I’ve never seen these "higher-level Busy Beavers" defined anywhere, probably because, to people who know computability theory, they’re a fairly obvious extension of the ordinary Busy Beaver numbers. So our reasonable modern mathematician wouldn’t know what number you were naming. If you want to use higher-level Busy Beavers in the biggest number contest, here’s what I suggest. First, publish a paper formalizing the concept in some obscure, low-prestige journal. Then, during the contest, cite the paper on your index card.
To exceed higher-level Busy Beavers, we’d presumably need some new computational model surpassing even Turing machines. I can’t imagine what such a model would look like. Yet somehow I doubt that the story of notational systems for big numbers is over. Perhaps someday humans will be able concisely to name numbers that make Busy Beaver 100 seem as puerile and amusingly small as our nobleman’s eighty-three. Or if we’ll never name such numbers, perhaps other civilizations will. Is a biggest number contest afoot throughout the galaxy?
¨
You might wonder why we can’t transcend the whole parade of paradigms, and name numbers by a system that encompasses and surpasses them all. Suppose you wrote the following in the biggest number contest: The biggest whole number nameable with 1,000 characters of English text Surely this number exists. Using 1,000 characters, we can name only finitely many numbers, and among these numbers there has to be a biggest. And yet we’ve made no reference to how the number’s named. The English text could invoke Ackermann numbers, or Busy Beavers, or higher-level Busy Beavers, or even some yet more sweeping concept that nobody’s thought of yet. So unless our opponent uses the same ploy, we’ve got him licked. What a brilliant idea! Why didn’t we think of this earlier?
Unfortunately it doesn’t work. We might as well have written
One plus the biggest whole number nameable with 1,000 characters of English text This number takes at least 1,001 characters to name. Yet we’ve just named it with only 80 characters! Like a snake that swallows itself whole, our colossal number dissolves in a tumult of contradiction. What gives?
The paradox I’ve just described was first published by Bertrand Russell, who attributed it to a librarian named G. G. Berry. The Berry Paradox arises not from mathematics, but from the ambiguity inherent in the English language. There’s no surefire way to convert an English phrase into the number it names (or to decide whether it names a number at all), which is why I invoked a "reasonable modern mathematician" in the rules for the biggest number contest. To circumvent the Berry Paradox, we need to name numbers using a precise, mathematical notational system, such as Turing machines—which is exactly the idea behind the Busy Beaver sequence. So in short, there’s no wily language trick by which to surpass Archimedes, Ackermann, Turing, and Rado, no royal road to big numbers.
You might also wonder why we can’t use infinity in the contest. The answer is, for the same reason why we can’t use a rocket car in a bike race. Infinity is fascinating and elegant, but it’s not a whole number. Nor can we ‘subtract from infinity’ to yield a whole number. Infinity minus 17 is still infinity, whereas infinity minus infinity is undefined: it could be 0, 38, or even infinity again. Actually I should speak of infinities, plural. For in the late nineteenth century, Georg Cantor proved that there are different levels of infinity: for example, the infinity of points on a line is greater than the infinity of whole numbers. What’s more, just as there’s no biggest number, so too is there no biggest infinity. But the quest for big infinities is more abstruse than the quest for big numbers. And it involves, not a succession of paradigms, but essentially one: Cantor’s.
¨
So here we are, at the frontier of big number knowledge. As Euclid’s disciple supposedly asked, "what is the use of all this?" We’ve seen that progress in notational systems for big numbers mirrors progress in broader realms: mathematics, logic, computer science. And yet, though a mirror reflects reality, it doesn’t necessarily influence it. Even within mathematics, big numbers are often considered trivialities, their study an idle amusement with no broader implications. I want to argue a contrary view: that understanding big numbers is a key to understanding the world. Imagine trying to explain the Turing machine to Archimedes. The genius of Syracuse listens patiently as you discuss the papyrus tape extending infinitely in both directions, the time steps, states, input and output sequences. At last he explodes.
"Foolishness!" he declares (or the ancient Greek equivalent). "All you’ve given me is an elaborate definition, with no value outside of itself."
How do you respond? Archimedes has never heard of computers, those cantankerous devices that, twenty-three centuries from his time, will transact the world’s affairs. So you can’t claim practical application. Nor can you appeal to Hilbert and the formalist program, since Archimedes hasn’t heard of those either. But then it hits you: the Busy Beaver sequence. You define the sequence for Archimedes, convince him that BB(1000) is more than his 1063 grains of sand filling the universe, more even than 1063 raised to its own power 1063 times. You defy him to name a bigger number without invoking Turing machines or some equivalent. And as he ponders this challenge, the power of the Turing machine concept dawns on him. Though his intuition may never apprehend the Busy Beaver numbers, his reason compels him to acknowledge their immensity. Big numbers have a way of imbuing abstract notions with reality.
Indeed, one could define science as reason’s attempt to compensate for our inability to perceive big numbers. If we could run at 280,000,000 meters per second, there’d be no need for a special theory of relativity: it’d be obvious to everyone that the faster we go, the heavier and squatter we get, and the faster time elapses in the rest of the world. If we could live for 70,000,000 years, there’d be no theory of evolution, and certainly no creationism: we could watch speciation and adaptation with our eyes, instead of painstakingly reconstructing events from fossils and DNA. If we could bake bread at 20,000,000 degrees Kelvin, nuclear fusion would be not the esoteric domain of physicists but ordinary household knowledge. But we can’t do any of these things, and so we have science, to deduce about the gargantuan what we, with our infinitesimal faculties, will never sense. If people fear big numbers, is it any wonder that they fear science as well and turn for solace to the comforting smallness of mysticism?
But do people fear big numbers? Certainly they do. I’ve met people who don’t know the difference between a million and a billion, and don’t care. We play a lottery with ‘six ways to win!,’ overlooking the twenty million ways to lose. We yawn at six billion tons of carbon dioxide released into the atmosphere each year, and speak of ‘sustainable development’ in the jaws of exponential growth. Such cases, it seems to me, transcend arithmetical ignorance and represent a basic unwillingness to grapple with the immense.
Whence the cowering before big numbers, then? Does it have a biological origin? In 1999, a group led by neuropsychologist Stanislas Dehaene reported evidence in Science that two separate brain systems contribute to mathematical thinking. The group trained Russian-English bilinguals to solve a set of problems, including two-digit addition, base-eight addition, cube roots, and logarithms. Some subjects were trained in Russian, others in English. When the subjects were then asked to solve problems approximately—to choose the closer of two estimates—they performed equally well in both languages. But when asked to solve problems exactly, they performed better in the language of their training. What’s more, brain-imaging evidence showed that the subjects’ parietal lobes, involved in spatial reasoning, were more active during approximation problems; while the left inferior frontal lobes, involved in verbal reasoning, were more active during exact calculation problems. Studies of patients with brain lesions paint the same picture: those with parietal lesions sometimes can’t decide whether 9 is closer to 10 or to 5, but remember the multiplication table; whereas those with left-hemispheric lesions sometimes can’t decide whether 2+2 is 3 or 4, but know that the answer is closer to 3 than to 9. Dehaene et al. conjecture that humans represent numbers in two ways. For approximate reckoning we use a ‘mental number line,’ which evolved long ago and which we likely share with other animals. But for exact computation we use numerical symbols, which evolved recently and which, being language-dependent, are unique to humans. This hypothesis neatly explains the experiment’s findings: the reason subjects performed better in the language of their training for exact computation but not for approximation problems is that the former call upon the verbally-oriented left inferior frontal lobes, and the latter upon the spatially-oriented parietal lobes.
If Dehaene et al.’s hypothesis is correct, then which representation do we use for big numbers? Surely the symbolic one—for nobody’s mental number line could be long enough to contain
Could early intervention mitigate our big number phobia? What if second-grade math teachers took an hour-long hiatus from stultifying busywork to ask their students, "How do you name really, really big numbers?" And then told them about exponentials and stacked exponentials, tetration and the Ackermann sequence, maybe even Busy Beavers: a cornucopia of numbers vaster than any they’d ever conceived, and ideas stretching the bounds of their imaginations.
Who can name the bigger number? Whoever has the deeper paradigm. Are you ready? Get set. Go.
References Petr Beckmann, A History of Pi, Golem Press, 1971.
Allan H. Brady, "The Determination of the Value of Rado’s Noncomputable Function Sigma(k) for Four-State Turing Machines," Mathematics of Computation, vol. 40, no. 162, April 1983, pp 647- 665.
Gregory J. Chaitin, "The Berry Paradox," Complexity, vol. 1, no. 1, 1995, pp. 26- 30. At http://www.umcs.maine.edu/~chaitin/unm2.html.
A.K. Dewdney, The New Turing Omnibus: 66 Excursions in Computer Science, W.H. Freeman, 1993.
S. Dehaene and E. Spelke and P. Pinel and R. Stanescu and S. Tsivkin, "Sources of Mathematical Thinking: Behavioral and Brain-Imaging Evidence," Science, vol. 284, no. 5416, May 7, 1999, pp. 970- 974.
Douglas Hofstadter, Metamagical Themas: Questing for the Essence of Mind and Pattern, Basic Books, 1985. Chapter 6, "On Number Numbness," pp. 115- 135.
Robert Kanigel, The Man Who Knew Infinity: A Life of the Genius Ramanujan, Washington Square Press, 1991.
Stephen C. Kleene, "Recursive predicates and quantifiers," Transactions of the American Mathematical Society, vol. 53, 1943, pp. 41- 74.
Donald E. Knuth, Selected Papers on Computer Science, CSLI Publications, 1996. Chapter 2, "Mathematics and Computer Science: Coping with Finiteness," pp. 31- 57.
Dexter C. Kozen, Automata and Computability, Springer-Verlag, 1997.
———, The Design and Analysis of Algorithms, Springer-Verlag, 1991.
Shen Lin and Tibor Rado, "Computer studies of Turing machine problems," Journal of the Association for Computing Machinery, vol. 12, no. 2, April 1965, pp. 196- 212.
Heiner Marxen, Busy Beaver, at http://www.drb.insel.de/~heiner/BB/.
——— and Jürgen Buntrock, "Attacking the Busy Beaver 5," Bulletin of the European Association for Theoretical Computer Science, no. 40, February 1990, pp. 247- 251.
Tibor Rado, "On Non-Computable Functions," Bell System Technical Journal, vol. XLI, no. 2, May 1962, pp. 877- 884.
Rudy Rucker, Infinity and the Mind, Princeton University Press, 1995.
Carl Sagan, Billions & Billions, Random House, 1997.
Michael Somos, "Busy Beaver Turing Machine." At http://grail.cba.csuohio.edu/~somos/bb.html.
Alan Turing, "On computable numbers, with an application to the Entscheidungsproblem," Proceedings of the London Mathematical Society, Series 2, vol. 42, pp. 230- 265, 1936. Reprinted in Martin Davis (ed.), The Undecidable, Raven, 1965.
Ilan Vardi, "Archimedes, the Sand Reckoner," at http://www.ihes.fr/~ilan/sand_reckoner.ps.
Eric W. Weisstein, CRC Concise Encyclopedia of Mathematics, CRC Press, 1999. Entry on "Large Number" at http://www.treasure-troves.com/math/LargeNumber.html.
sábado, 25 de junho de 2011
Solucionando o Insolucionavel (Solving the Unsolvabe)
Fonte aqui
O (não*) deixei aqui por achar que houve erro na redação original do texto, mas deixo a intepretação para vocês e concluam se é necessário ou não. Caso queiram alguma coisa de links relacionados, podem deixar nos comentários que tentarei colocar algo sobre alguma coisa do que foi citado no texto.
terça-feira, 5 de abril de 2011
Seleção de Páginas, blá-blá-blá etc. e tal
Buenas. Fiquei vários dias sem nova postagem e devendo a seleção de páginas votada por unanimidade :P. Colocarei os links para páginas selecionadas e as de jogos que rodem em browser também porque seria postados depois por mim de qualquer modo. Os links para essas seleções serão disponibilizados na área de links lateral para organizar esta birosca. Novas mudanças para os posts serã anunciadas no dia da alteração pra facilitar a vida do mundo :)
Provavelmente adotarei um novo lugar para posts, darei o aviso aqui quando estiver pronto.
Provavelmente adotarei um novo lugar para posts, darei o aviso aqui quando estiver pronto.
Jogos Livres de Instalação em Disco
(podem precisar do "prugin do Frash" ou algo parecido)
Isolados:
Auditorium - Index
Entanglement
Elements the Game
Coleções:
The Smart Ass
New Grounds
Kongregate Games
Isolados:
Auditorium - Index
Entanglement
Elements the Game
Coleções:
The Smart Ass
New Grounds
Kongregate Games
Esportes, Artes Marciais e Luta
Capoeira
Capoeira Science
Corrida:
Longão: O que é pisada pronada, normal e supinada?!
Kung Fu:
Academia Wu Song de Kung Fu
RED PALM CLAN 紅掌派
Taekwondo:
Sun-Do Taekwondo - Philosophy of Taekwondo
Philosophical Principles of Taekwondo
Active Taekwondo (blog Active Taekwondo)
Capoeira Science
Corrida:
Longão: O que é pisada pronada, normal e supinada?!
Kung Fu:
Academia Wu Song de Kung Fu
RED PALM CLAN 紅掌派
Taekwondo:
Sun-Do Taekwondo - Philosophy of Taekwondo
Philosophical Principles of Taekwondo
Active Taekwondo (blog Active Taekwondo)
Comércio
Informática:
[D]Ferrari TUDO EM INFORMÁTICA - LISTA 1° PAG. PEÇAS - NOTEBOOKS - CONSOLES (fórum Adfrenaline)
Promoções/Bons Preços na Internet - Fórum do Clube do Hardware (fórum Clube do Hardware :P )
[D]Ferrari TUDO EM INFORMÁTICA - LISTA 1° PAG. PEÇAS - NOTEBOOKS - CONSOLES (fórum Adfrenaline)
Promoções/Bons Preços na Internet - Fórum do Clube do Hardware (fórum Clube do Hardware :P )
Assinar:
Postagens (Atom)